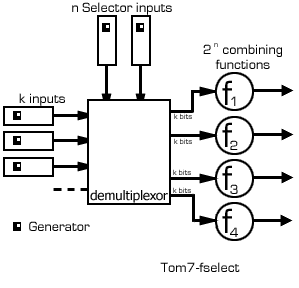This is a method of combining generators of any sort (in the code below I use LFSRs) in a way which increases the complexity of the system.

The basic idea is to use a multiplexor with k input generators and n selector generators to select between 2ⁿ combining functions to combine the k bits. The output is the output of this function.

For the functions given and used below, k must be odd. I've used 4 functions in my implementation and five input bits, so n=2 and k=5. The functions are threshold, xor, overflow-sum, and inverse threshold.

The initial state of the generators is determined by the key, and the generators are also clocked a certain number of times based on the key to initialize them. In the implementation below, I cycle through the 7 generators and fill each of their 4-byte data from msb to lsb from the key (cyclically), and then use a fifth byte and clock the generator that many times. This implies a maximum key length of 5*7*8=280 bits; shorter keys are repeated to make the requisite 35 bytes.

Each function must produce a bit with even distribution based on the k input bits. The functions used are:

• threshold: the output is the majority function; if there are more than half 1's it outputs 1, else 0.
• xor: this is the exclusive or of all the bits.
• overflow-sum: incoming bits are added to a 3 bit register with overflow (adding 1 to 111 produces 000). Output is the least significant bit. The register retains its contents between outputs.
• inverse threshold: this is the binary complement of the threshold function.

Analysis

Using my program stat, this produces well-distributed pseudo random bits for a variety of keys (up to degree 7). This is by no means a thorough test, but it performs as expected, at least.

Breaking the generators sequentially could reasonably lead to breaking the cipher. Since there is no feedback mechanism, a generator which you have 'solved' always produces the same output. The output of any generator is heavily obscured by the others, but a probabilistic attack could work with a known-plaintext scenario (given that I know my solved generator output 1, and the entire device output a 0, what is the probability that generator x output a 1?, etc.) Since the initial state of a generator only depends on 5 bytes (= 40 bits) of the key, this especially facilitates an attack. Knowing n-1 generators does not even mean you necessarily know the output of the final generator (when either threshold function is used, there are times when the output of a single generator does not matter (all the others have voted 1, for instance). It seems like a difficult attack to mount and I wouldn't know where to start, but it is a weakness nonetheless.

Improvements

The code below uses generators with periods which are not all relatively prime. I highly recommend using generators which are; my source of data Applied Cryptography did not have enough.

Some sort of feedback to the generators would be useful. It seems to make it inelegant, but a skipstate-type feedback from the output and between the generators would probably hinder cryptanalysis.

LFSRs are considered insecure and should not be used.

A key scheme in which each key bit affected each generator's state would be especially useful. I have used the method described above in the interest of simplicity, but do not recommend it.

Implementation

/*
   C Implementation of Tom7-fselect stream cipher.
   This code is distributed under the GNU public license;
   see http://www.gnu.org/copyleft/gpl.html.

   I can't make any claims about the security of this algorithm because
   I am not a trained cryptographer, though it produces (as far as I can
   tell) statistically random output. This code should be thought about,
   but not used unless you know more about this than me.

   The biggest fault I see with this is that the generators are not
   all relatively prime in length -- Applied Cryptography did not have
   enough given for me to pick 7 that were. The period is still something
   pretty huge, at least 2^127 bits before it repeats.

     Tom 7

   http://tom7.org/

*/

#include 

typedef struct {
     unsigned long data;
     unsigned long mask;
     unsigned char len;
} LFSR;

int func_thresh(char * bits);
int func_xor(char * bits);
int func_sum(char * bits);
int func_notthresh(char * bits);

unsigned char generator(LFSR * gen);

int (*func[])(char * bits) = {
     func_thresh,
     func_xor,
     func_sum,
     func_notthresh,
};

LFSR G[7] ={
     {0,(1<<31)|(1<<6)|(1<<4)|(1<<2)|(1<<1)|1,31},
     {0,(1<<29)|(1<<5)|(1<<3)|1,29},
     {0,(1<<30)|(1<<12),30},
     {0,(1<<18)|(1<<4)|(1<<1)|1,18},
     {0,(1<<16)|(1<<4),16},
     {0,(1<<12)|(1<<3)|(1<<2)|1,12},
     {0,(1<<31)|(1<<6)|(1<<2)|(1<<1)|1,31},
};

unsigned char SUM_CARRY=0;
#define CARRY_LEN 7  /* that's 111 binary, not 7 bits. */

/* G[5], G[6] are selector bits for the functions.
   G[0] through G[4] are the inputs for f[0,1,2,3] */

main (int argc, char**argv) {
   unsigned char bits[5], output, *key;
   unsigned int x,z,a,s,c;

   if (argc>=2) key = argv[1];
      else { printf("%s key [bits]\n",argv[0]); exit(-1); }
    
   s = strlen(key);
   for (x=c=0;x<7;x++) {
        G[x].data |= key[c++%s] << 24;
        G[x].data |= key[c++%s] << 16;
        G[x].data |= key[c++%s] << 8 ;
        G[x].data |= key[c++%s]      ;
        a = key[c++%s]; while (a--) generator(&G[x]);
   }
   if (argc>=3) z = atoi(argv[2]); else z=1000;

   while (z--) {
        for(x=0;x<5;x++) bits[x] = generator(&G[x]);
        output = func[(generator(&G[5])<<1)|generator(&G[6])](bits);
        putchar('0'+output);
   }
}

int func_thresh(char * bits) {
     int c=0,x;
     for(x=0;x<5;x++) if (bits[x]) if (++c==3) return 1;
     return 0;
}
int func_xor(char * bits) {
     int c=0,x;
     for(x=0;x<5;x++) c ^= bits[x];
     return c&1;
}
int func_sum(char * bits) {
     int c=0,x;
     for(x=0;x<5;x++)
          if (bits[x]) if (++SUM_CARRY>CARRY_LEN) SUM_CARRY=0;
     return SUM_CARRY&1;
}
int func_notthresh(char * bits) { 
     int c=0,x;
     for(x=0;x<5;x++) if (!bits[x]) if (++c==3) return 1;
     return 0;
}

unsigned char generator(LFSR * g) {
     if (!g->data) g->data++; /* keys of all 0's ruin LFSRs */
     if (g->data & 1) {
          g->data = ((g->data ^ g->mask) >> 1)
               | (1<len); /* g->len is already len-1 */
          return 1;
     } else {
          g->data>>=1; return 0;
     }
}

Back to Tom's Cryptography Thingie.
Back to Tom's CMU Page.